3 thoughts on “反比例”

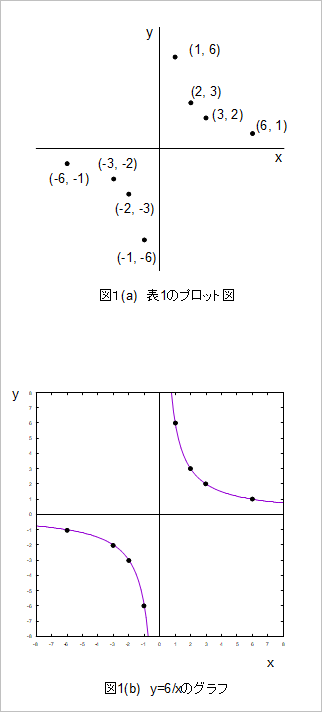
1. ≪…比例と反比例という対立する言葉で表現…≫をウマクウマク纏め上げ普遍言語化しているのが［数の言葉ヒフミヨ（１２３４）］である。

   返信

2. 　≪…比例と反比例という対立する言葉で表現…≫を内在化している眺望は、「数のヴィジョン」になるとか・・・

   　自然数のキュレーション的な催しがあるといいなぁ～

   返信

3. 　≪…比例と反比例…≫を、数学からの送り返して来たモノとして眺めると・・・
   自然数の創生に・・・

   ・・・　・・・　・・・　
   1. 数学的な定義：円錐曲線の一つ
   双曲線は、数学では円錐曲線の一つとして定義されます。
   円錐曲線を理解するには、円錐をイメージし、それを平面で様々な角度で切断したときの断面を考えると分かりやすいです。

   円: 垂直に切断した断面。
   楕円: 斜めに切断した断面（軸に対して）。
   放物線: 軸と平行に切断した断面。
   双曲線: 軸と垂直ではない角度で、円錐の二つの部分をどちらも横切るように切断したときに現れる、二つの対になった曲線です。

   この二つの対になった曲線は、それぞれが広がり続け、無限に遠ざかっていきます。

   2. 天文学的な意味：「脱出」の証明
   天文学において、天体の軌道形状は、その天体の離心率 (e)という値によって決まります。これは、天体が中心天体の重力にどれだけ強く「束縛されているか」を示す指標です。
   双曲線とは (1)

   3I/ATLASなどの恒星間天体は、太陽系とは無関係の遥か遠い別の恒星系から、非常に速いスピード（脱出速度以上）で太陽系に進入してきました。

   そのため、太陽の重力ではその進路を少し曲げることしかできず、重力的な束縛を受けません。その軌道はe > 1 の双曲線となり、一度太陽の近くを通過すると、そのまま二度と戻ることなく銀河系の彼方へと去っていくのです。

   これが、双曲線軌道を持つ天体を「宇宙の旅人」と呼ぶ理由です。
   ・・・　・・・　・・・　
   ［　離心率 (e)　］が、数の言葉（自然数）とインターラクトしている気付きを教えていただきありがとうございます。
   　標高差が光格子時計でワカル時代になり、［数の旅人］もこんなように想います。

   　円（コスモスな自然数）　　⇒　　放物線（2次方程式）　⇒　双曲線（反比例曲線）　

   　この旅路を逆に辿ると数の言葉ヒフミヨからの自然数の眺めに。

   直交座標での反比例曲線を４５°（π/4）回転の操作すると、双曲線と漸近線（正比例直線）の眺めに、反比例曲線と正比例直線とのインターラクトが数の言葉の旅路の始まりに。

   そして、２次方程式の因数分解と円のインターラクトが放物線の焦点と準線で直交座標を成り立たせている。

   直交座標から切り出された『自然比矩形』（1×(e-1））と円のインターラクトが4次元で閉じている数の言葉ヒフミヨからの自然数の眺めに、≪…離心率…≫をあらためて想う・・・

   　［ヒト］の脳は、重力を無意識に深く深く取り込んでいるのだろう・・・

   返信