カテゴリー
目次
オートポイエーシス入門
1 定義
2 概念
3 三つのシステム
- オートポイエーシス論の適用
- 細胞システム
- 多細胞生命体システム
- 生命現象のオートポイエーシス論的説明
- 心と身体の関係
- 意識システム
- 認識システム
- 言語に関連する事項
- 社会をシステムとしてみる
- ルーマンの社会システム論
4 オートポイエーシス論の展開
- オートポイエーシス論の展開のために
- コード再考
- 意識システムの模式図
- 動物行動(オートポイエーシス論)
- オートポイエーシス論によるゲシュタルト知覚
- ルーマンの縮減概念
- 本能行動と欲求行動
- 知能行動(オートポイエーシス論)
- 世界像(オートポイエーシス論)
哲学入門
1 古代
- 哲学の始原
- あるということ
- 古代原子論
- 知を愛すること
- ソクラテスのアイロニー
- プラトンのイデア論
- アリストテレスの形而上学
- ヘレニズム期の哲学
- 古代の懐疑論
- 一者の思考(新プラトン主義)
- キリスト教神学へ
- 古代の哲学から中世の哲学へ
- 古代の哲学まとめ
2 中世
3 近代
- 近代の哲学を読むにあたって
- 機械論的自然観
- デカルトのコギト
- 基体としての人間理性
- 近代形而上学のイデア的認識
- 経験論の形成
- イデアへの反抗
- イギリス経験論の展開
- モナド論
- 人間理性の限界
- 自己を認識する自己
- 近代形而上学の完成
- 同一性と差異
- 生成する自然(後期シェリング)
- マルクスの哲学
- 力への意志
- 近代の哲学まとめ1(知覚・認識論)
- 近代の哲学まとめ2(西洋近代形而上学)
- 近代の哲学まとめ3(自然科学と形而上学)
心理学入門
〇ゲシュタルト・クライス
〇アフォーダンス
- 「アフォーダンス入門」について
- アフォーダンスの定義
- アフォーダンス概念からの展開
- ブルート・ファクツ(ありのままの運動)
- 動物が自ら作り出す意味
- 環境と接することとしてあるこころ
- 子供の言葉と周りにある「意味」
〇動物行動学
学術分野一般
〇民主主義
中学数学を理解する
〇一年
〇二年
- 分配法則
- 二元一次連立方程式
- 代入法(二元一次連立方程式の解き方1)
- 加減法(二元一次連立方程式の解き方2)
- 連立方程式の利用
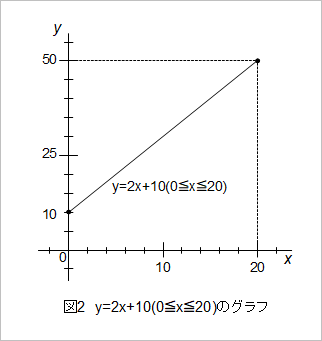
- 一次関数
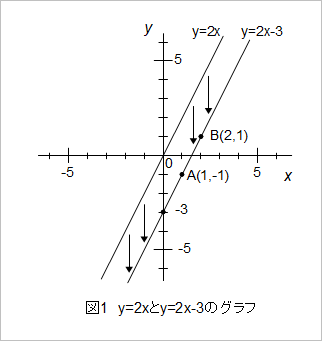
- 二元一次方程式と一次関数
- 二つの一次関数の交点の座標
- 図形の証明における命題の利用
- 三角形の合同の証明
- 和の法則と積の法則(場合の数)
- 確率
〇三年
高校数学を理解する
数Ⅰ
〇二次関数
〇三角比
数A
〇確率
数Ⅱ
〇三角関数
- 角度表現の変更と拡張
- 三角比の拡張(ラジアン表示)
- 三角関数の公式1
- 三角関数の公式2
- 三角関数のグラフ
- タンジェント関数のグラフ
- 三角方程式の角度の拡張
- 三角比の不等式
- 加法定理
- 倍角の公式と半角の公式
- 三角関数の合成
数B
〇数列
〇ベクトル
- ベクトルとは
- ベクトルの演算規則
- ベクトルの成分表示と単位ベクトル
- ベクトルの内積
- 位置ベクトル
- 同一直線上の三点のベクトル表現
- 直線のベクトル方程式
- 方向ベクトルと法線ベクトル
- 空間ベクトル
- 空間における平面と直線の方程式
- ベクトルの利用
〇確率分布
数Ⅲ