ベクトルの演算規則
前回ベクトルがどういうものとして定義されているか説明しました。一つ忘れていたのが、ベクトルは自由に平行移動可能だという性質をもつことです。場所を固定して考える位置ベクトルもあるのですが、いったんそうさせてください。それで今回は、ベクトルの記述と演算規則についてです。
1.ベクトルの実数倍
前回述べた通り、ベクトルは「向きと大きさを持つ量」です。ここから次の二つの規則がそのまま生まれてきます。
- あるベクトルに実数をかけると、もとのベクトルに対して大きさが実数倍になる。
- あるベクトルに-1をかけるとベクトルの向きが逆になる。
説明のためにベクトルの実数倍に関する記述方法を示しておきます。
\begin{align} k\overrightarrow{AB} \end{align}
のようにABベクトルの頭にkをつけることで、ABベクトルのk倍のベクトルを表現します。
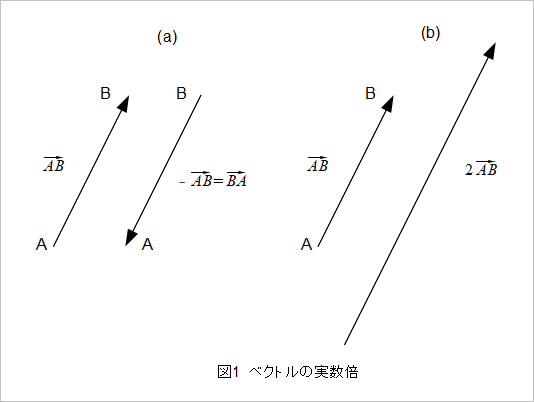
-ABベクトルならABベクトルの-1倍で、2ABベクトルならABベクトルの2倍です。-ABベクトルはABベクトルに-1をかけているので、この二つのベクトルの関係は図1(a)のような同じ大きさで逆方向のベクトルになります。始点がB、終点がAに変わっているのでBAベクトルでもあります。また2ABベクトルは図1(b)のようにABベクトルと同じ向きで2倍のベクトルです。
2.ベクトルの加算と減算
次はベクトルの加算と減算についてです。先に数式表現を下に示します。
\begin{align}
1. 加算:\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\\
2. 減算:\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}
\end{align}
式だけ見るとなにがなんだがわからない計算規則だと思います。まず加算から見ていきましょう。
2.1 ベクトルの加算
加算は図2のように図示できます。前回でも述べましたが、ベクトルは平行四辺形の対角線との関係で考えるといくらか理解しやすくなります。図2のようにABベクトル(aベクトルとします)とBCベクトル(bベクトルとします)を加算するとき、この二つのベクトルを使って平行四辺形を作り、その対角線が加算された後のベクトルになります。二つのベクトルを足すときは、一つ目のベクトルの始点から二つ目のベクトルの終点をつなぐ一つのベクトルになる、と覚えるとよいでしょう。
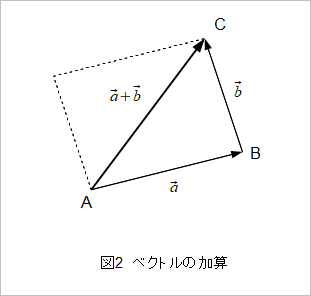
この加算の規則はベクトルを成分表示してみればよくわかります。図2の二つのベクトルを成分表示するとaベクトル=(4,1)、bベクトル=(-1,3)です。直交するxとyの軸に分けているのだから、xはx、yはyで分けて加算を考えればよさそうです(図3)。
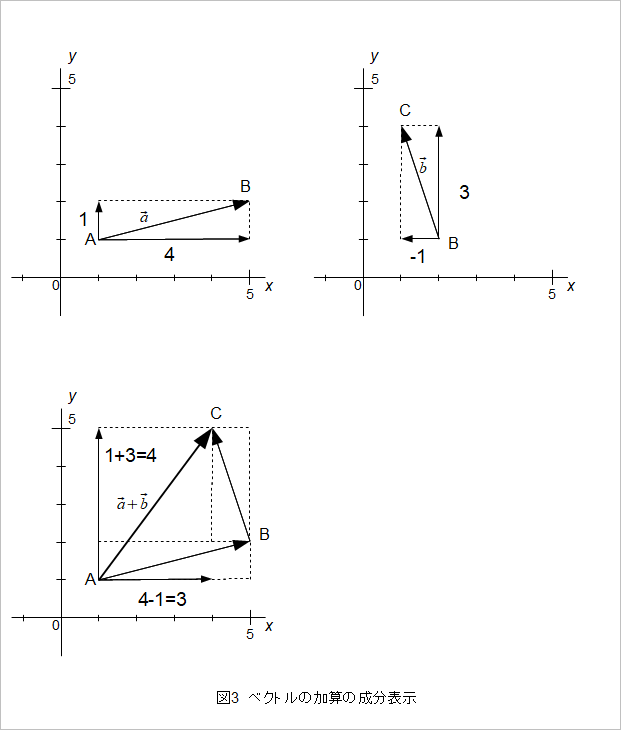
aベクトルのx成分は4でbベクトルのx成分は-1なので、これを足し合わせて4+(-1)=3です。aベクトルは水平方向では右向き(正方向)で大きさ4、bベクトルは水平方向では左向き(負方向)で大きさ1なので、右向きと左向きを足すので大きさが打ち消して、aよりは小さい大きさ3の右向きとなります。また、aベクトルのy成分は1でbベクトルのy成分は3なので、これを足し合わせて1+3=4です。aベクトルもbベクトルもy成分は上向き(正方向)なので、上向きと上向きを足してさらに大きくなって上向きに4です。成分ごとに加算した結果はaベクトル+bベクトル=(3,4)となり、図2のACベクトルと一致しています。
2.2 ベクトルの減算
ベクトルの減算も成分表示で考えることができるのですが、せっかく加算で図形的に足して一つになると示せているので、ここでは図形的に考えてみることにします。-bベクトルというのはACベクトルと同じ大きさの逆向きのベクトルなので、CAベクトルです。
\begin{align}
\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{AB}+(-\overrightarrow{AC})\\ =\overrightarrow{AB}+\overrightarrow{CA}
\end{align}
ということなので、図4のCAベクトルをBを始点にして平行移動すると、この二つのベクトルの減算結果は、加算の規則(図2)を適用して、ADベクトルになるのがわかります。
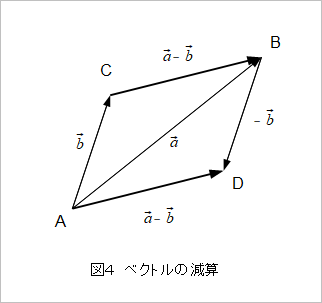
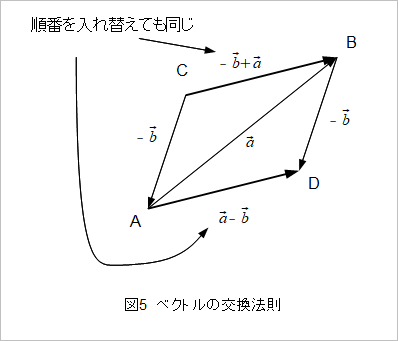
結果としてできたこの図形は平行四辺形になっているので、ADベクトルはCBベクトルと平行で同じ大きさです。したがってADベクトル=CBベクトルより、ABベクトル-ACベクトル=CBベクトルになります。平行移動しても同じベクトルということは交換法則がなりたっていることを示しているので(図5)、次に計算するときはABベクトル+CAベクトル=CAベクトル+ABベクトルのように順番を入れ替えて、始点と終点よりCBベクトルだと考えた方が見つけやすいかもしれません。
\begin{align}
\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{AB}+(-\overrightarrow{AC})\\ =\overrightarrow{AB}+\overrightarrow{CA}\\
=\overrightarrow{CA}+\overrightarrow{AB}\\
=\overrightarrow{CB}
\end{align}
3. ベクトルの演算規則
最後にベクトルの計算法則とベクトルの平行の記述方法をまとめておきます。
\begin{align}
\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{c}\\ (\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\\ (kl)\overrightarrow{a}=k(l\overrightarrow{a})\\ (k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}\\ k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b}\\ ベクトルの平行:\overrightarrow{a}/\!/\overrightarrow{b} (ただし\overrightarrow{a}\ne\overrightarrow{0},\overrightarrow{b}\ne\overrightarrow{0})\\ ベクトルの平行条件:\overrightarrow{a}/\!/\overrightarrow{b}\rightleftarrows \overrightarrow{b}=k\overrightarrow{a}
\end{align}
これらの規則は交換法則や分配法則とそれに関係する規則で、これまでの実数の演算と同じ規則が成り立ちます。ベクトルの定義を振り返ってみれば、この規則が成り立つことに特に違和感は感じないと思います。
またベクトルの減算と加算を成分表示で表すと、aベクトル=(a,b)、bベクトル=(c,d)のとき
\begin{align}
\overrightarrow{a}+\overrightarrow{b}=(a, b)+(c, d)\\ =(a+c, b+d)\\ \overrightarrow{a}-\overrightarrow{b}=(a, b)-(c, d)\\ =(a-c, b-d)\\
\end{align}
のようにそれぞれの成分ごとに数値計算することで求められます。
<< ベクトルとは ベクトルの成分表示と単位ベクトル >>




