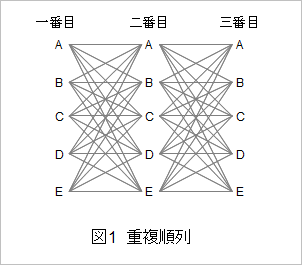
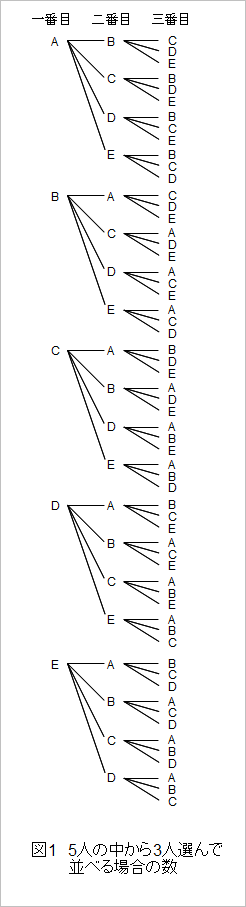
動物行動を説明することにおいて、対立的な考え方がいくつかあって、それらはだいたい生理学的または心理学的な概念です。生理学や心理学を無視して動物行動を説明するのは無理なので、それらの考え方のいくつかをざっと示しておこうと思います。
上で述べたような対立的に使用される言葉として、「生得説と習得説」、「外からのアプローチと内からのアプローチ」、「極所論と全体論」、「内部精神物理学と外部精神物理学」など、まあたくさんあります。これらの概念の対にはつながりがあって、ある立場の人はこの組み合わせといった感じに、ある種の派閥が形成されていたりします。動物行動の具体的説明の前に、これらの概念対について簡単に見ておきましょう。これらの概念自体がある考え方を反映してくれているので、考え方全体を概観する手助けになってくれるはずです。
1.概念対の説明
1.1 生得説と習得説
動物行動は生得的に固定されたものか、後天的に習得されるものか、という議論だと思ってください。本当は単純な話ではないんですがあえて単純化すると、たとえば「本能行動」は種ごとに生得的に決定された行動で、「学習」は後天的に獲得された、もしくは変化した行動です。ある程度神経系の発達した動物なら、本能行動も学習も両方の行動を取ることに異論はないと思います。これだけだと何の問題もないように見えますが、動物行動学の根幹をなすような複雑な様相を呈するので、これは別のページで説明する予定です。
1.2 外からのアプローチと内からのアプローチ
動物は基本、ある行動から次の行動へと行動を連接し続けることで生活しています。ある行動と他の行動の区別はそんなに峻別できるものかという疑問は生じますが、たとえば求愛行動とか、確かにそれとして人の目に現れてくる行動があります。それぞれの行動として区切ることが可能だとして、生物学では一般に外部刺激の入力を始発項として行動として外部に出力される、と考えます。高校生物なんかは完全にこの考え方を採用しているのですが、実際には生体内部の自律的作動が同じくらいに重要です。簡略化せざるを得ない「高校生物」では仕方ないと思うのですが、「入力・出力」モデル以外の考え方が浮かばなくなってしまう危険性はあるでしょう。
上の事柄に関連して、動物行動の始発項を外部に置くか内部に置くかの違いによる、「外からのアプローチ」と「内からのアプローチ」の二つの立場があります。図1にこの二つの考え方の略図を示しておきます。一見、始発項を外部に置くか内部に置くかだけの図に見えますが、他の対立項の出発点をも含んでいます。
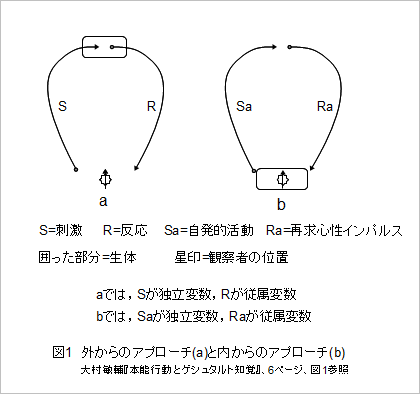
連接・循環しているはずの動物行動をどう区切るかという話に戻ると、生体の外からその生体を観察するのか、生体の側から考えるかで変わってきます。図1の(a)「外からのアプローチ」は観察者が生体の外にいて、与えた刺激にどう反応するかという考え方を反映しています。動物行動を観察することは動物行動学の基本であるのは今でも変わらなくて、人間が動物行動を観察するのだから(a)の外からのアプローチ以外にあり得ないようにも思えます。しかし人間が確実に観察できるのは動物の行動だけです。その行動の意味を観察者が読み取るのに、動物の主体や心的現実(意識やこころへの現れ)を無視して動物にとっての意味を読み取れるものでしょうか。
生体の主体の側からの視点で考えられているのが(b)「内からのアプローチ」です。生体の内側から観察することが可能かという問題点があって、その一つの答えが生理学的機構と平行しながら観察することと言えます。図1(b)に「再求心性インパルス」という生理学的概念が突如出てきているのは、そんな事情を反映してだと思われます。再求心性インパルス説についてはページを改めて説明します。
1.3 内部精神物理学と外部精神物理学
「平行論」と呼ばれる、身体という物理的構造の状態と平行して心的現実が現れる、とする立場があります。身体(特に神経系)と心的現実の対応を認めながら単純な因果関係を否定する立場といってもよいでしょう。「外からのアプローチ」にしろ「内からのアプローチ」にしろ、行動時の主体における「観察可能な」何かを調べる必要があります。主体の心的現実の現れが本当に知りたいものだとしても、この現れは外部からは観察不能なので、心的現実と平行して現れる「生理学的(特に神経系の)変化」や「外部に表出される行動」を観察することになります。心的現実と身体内部の対応関係をみたのが内部精神物理学で、身体外部の行動との対応関係をみたのが外部精神物理学です。前者の代表格にゲシュタルト心理学、後者の代表格に認知心理学が挙げられます。それらの理論を押し進めた代表的な研究者たちが反目していたわけではないのですが、その後対立的な関係になって現在は後者の行動主義的な立場が優勢になっているという事情があります。
1.4 局所論と全体論
神経生理学というか、脳科学あたりで割と目にする概念です。高等哺乳類くらいでは、大脳皮質のどの部位はどういう役割を担うかというのがだいたい決まっています。批判を恐れずに簡略化して言えば、局所論は局所的に役割が決まるのだから各領域を調べれば脳機能が解明できるという立場で、全体論は他領域との関わり合いの中でその領域の役割が決まっているのだから全体との関係も考慮しないといけないという立場です。相手の考え方を理解しないまま不毛なすれ違いが起こっていることが多いので、これらの言葉が出てきたらそのことに注して読む必要があります。
2.多数の概念の絡まり合い
それぞれの概念対どうしにおいて相性のよい組み合わせがあったりします。上で示した概念で言えば、たとえば「外からのアプローチ」、「外部精神物理学」、「局所論」の組み合わせで考えている人が一番多く見られる感じです。ある概念が他の概念に関わる議論から考え出されたという場合もあるので、こういった親和性が現われるのも当然でしょう。一方で異なる経緯で出てきた概念が意図しない形で接続されたりすることもあって、けっこう錯綜している場合も見受けられます。ここで説明できたらよかったんですが私の能力を超えるのでここまでにさせてもらいます。
その研究者がどの立場をとっているかは本人が気づいているかどうかにかかわらず、その論文や著書を読み解くのに必要になってきます。動物行動に関わる研究では、どれかの立場を取ることなしに実験結果を解釈することも難しいです。動物行動に関する言説に触れるときは、その人の考え方がどういう立場に基づいているのかも考慮に入れる必要があります。
<< 脊椎動物の身体 脊椎動物の身体動作 >>