趣味で学問

条件付き確率

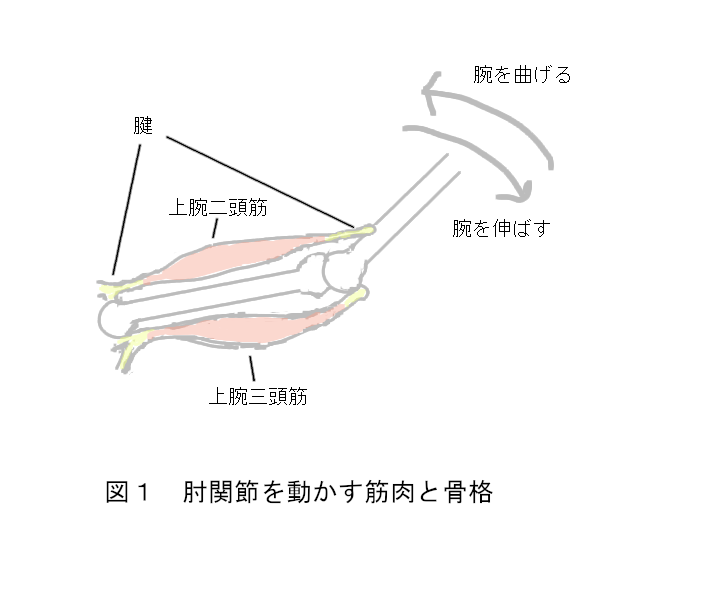
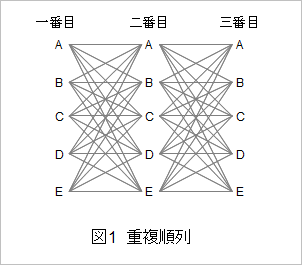
高校数学の確率において理解が難しいものの一つに条件付き確率があります。これはある事象が起こった後、その後に起こる事象の確率が前の事象の結果に左右される場合です。日常的には出来事とはそのようなものに思えますが、あらためて確率として考えると頭が痛くなる事態が待っていたりします。

まずは記号と式の定義を先に書いておきます。事象Aが起こったという条件のもとに事象Bが起こる条件付き確率をP_A(B)またはP(B|A)と書きます。どちらもよく使われるのですが、高校数学ではP_A(B)が使われることがほとんどですので、このページではこちらを使うことにします。条件付き確率P_A(B)は次のように式で表せます。

\begin{align} P_A(B)=\frac{P(A \cap B)}{P(A)}…①\\ P(A)P_A(B)=P(A \cap B)…②\\ \end{align}

個人的には②の方が覚えやすくて、こちらを覚えておけば両辺をP(A)で割れば①の式も出てくるので、下を覚えて必要があれば式変形するので構わないと思います。②の式では「A∩B」は「Aが起きてAが起きた条件でBが起きる」のと同じという意味が読み取れます。もしAが起きることがBに影響しない、つまりAとBが独立ならP(A∩B)=P(A)P(B)なので、独立な場合の式と比較すると②の式は覚えやすいと思います。

条件付き確率の問題を解く場合、条件付き確率をそのまま考えればあっさりわかる問題と、上記の式をもとに計算していかないといけない場合があります。ここでは条件付き確率をそのまま考えることのできる場合の例を1題示します。

「12本の中に当たりが4本入っているくじがあるとします。AとBがこの順でくじを引くとき、Aがあたる事象をA、Bがあたる事象をBとおいて条件付き確率を考えます。ここではAが当たった条件でBが当たる確率を求めます。」

Bが引くときにはすでにAが引いて当たりを引いているので、11本のくじの中に当たりが3本ある状態で引きます。よってAが当たった条件でBが当たる確率P_A(B)は3/11です。気を付ける必要があるのは、P_A(B)はあくまでBが当たる単独の場合の確率で、Aが当たってかつBも当たる確率P(A∩B)の場合ではないことです。この確率は②の式で計算でき、P(A∩B)=P(A)P_A(B)=(4/12)×(3/11)=1/11となります。これは直観的にも納得のいく計算になっています。式の形から三つ項のうち二つが分かれば残り一つもわかるので、P(A∩B)を求めるのにP_A(B)を利用してもよいし、P_A(B)を求めるのにP(A∩B)を利用してもよいです。でもこの問題ではP(A∩B)を求めるのが大変で、P_A(B)を式ではなく直接考えた方が早いです。

問題を解くだけならこれで終わりでよいのですがもうちょっと考えてみます。Bが当たる確率P(B)はどう考えればよいでしょう。さっきP_A(B)を計算したので、これにAが外れた条件でBが当たる確率P_Aバー(B)を計算して足してやると、P(B)=3/11+4/11=7/11となりそうな気がします。でも12本のうち4本当たり（Aの結果により若干変わりますが）のくじから1本のくじを引いてそれが4/12より明らかに大きな7/11の確率というのは納得がいかないです。

何の考慮が足りなかったかというと、Aが先にくじを引いてしまっていることの考慮です。Bがくじを引くというのは、Aがくじを引いてかつBが続けてくじを引くと考える必要があります。したがってP(B)=P(A∩B)+P(Aバー∩B)の式で考えることになります。計算を下に示します。

\begin{align} P(A)=\frac{4}{12}=\frac{1}{3}\\ P_A(B)=\frac{3}{11}\\ P(A \cap B)=\frac{4}{12}\cdot\frac{3}{11}=\frac{1}{11}\\ P(\overline{A})=\frac{8}{12}=\frac{2}{3}\\ P_\overline{A}(B)=\frac{4}{11}\\ P(\overline{A} \cap B)=\frac{8}{12}\cdot\frac{4}{11}=\frac{8}{33}\\ P(B)=P(A \cap B)+P(\overline{A} \cap B)\\ =\frac{1}{11}+\frac{8}{33}=\frac{11}{33}=\frac{1}{3}\\ \end{align}

計算の結果出てきた値は1/3、つまり先に引くAも後に引くBも結局は同じ確率になる、ということです。Aの結果によりBの結果が変わると言っても、Aの結果は偶然で決まるのだから次に引くBが当たる確率も結局はAと同じく偶然同じ値に決まる、ということを言っていると解釈すれば納得できる気もします。

もう一つ、P_B(A)はどうなのか考えてみます。P(A∩B)とP(B∩A)は同じなので、②の式でAとBを入れ替えてP(B)P_B(A)=P(B∩A)が成り立つはずです。ところでP_B(A)をどう解釈すればよいでしょうか。順番としてはAが先に起こって次にBが起こるので、「Bが起こったとわかった上で先に起こったAの確率」と考えればよさそうです。P(A∩B)=P(B∩A)、先ほど計算したP(B)を使って、P_B(A)を計算してみます。

\begin{align} P(B)=\frac{1}{3}\\ P(B \cap A)=\frac{1}{11}\\ P_B(A)=\frac{\frac{1}{11}}{\frac{1}{3}}=\frac{3}{11}\\ \end{align}

このようにある結果がわかった後で先の確率を推測することが可能です。さらにP_B(A)=3/11でP_A(B)と同じ値になっています。これもP(A)=P(B)となるのと同じ考え方ができそうですが、なんだかよくわからない感じが残ります。このわからなさは、本当に数学感覚のある人以外は、これからずっと付き合うことになると思います

<< 反復試行の確率

反復試行の確率

同じ試行を何度か繰り返すときの確率を反復試行の確率といいます。ある試行が次の試行に影響するわけではないので、独立試行の確率の一例ともいえますがあまり気にしなくてよいかもしれません。まずは定義を先に書いておきます。n回同じ試行を繰り返すとき、事象A（その確率はp）がr回出るときの確率は以下の通りです。

\begin{align} {}_n \mathrm{C}_r p^r (1-p)^{n-r} \end{align}

具体例の方がわかりやすいでしょうから、サイコロを続けて何度か振る場合で説明してみます。「サイコロを3回振って、1または2の目が2回出る確率」を知りたいとします。サイコロを1回振って1または2の目が出る確率は、2通り/全6通り=1/3です。1または2の目が出ない確率は1-1/3=2/3です（余事象）。サイコロを3回振って、1または2の目が2回出て3から6までの目が1回出るということですから、1/3×1/3×2/3で2/27の確率に思えます。1回目と2回目に出て3回目に出ないという確率ならこの値で正しいです。実際には1回目と3回目、2回目と3回目に出る場合もあるので、この3通りの確率を足す必要があります。1回目と3回目に出る場合の確率は1/3×2/3×1/3で、さきほどと同じ2/27になります。残り一つの場合でも同じです。今計算したことを表にまとめてみます。

	1回目	2回目	３回目	確率
(a)一通り目	〇(1/3)	〇(1/3)	×(2/3)	2/27
(b)二通り目	〇(1/3)	×(2/3)	〇(2/3)	2/27
(c)三通り目	×(2/3)	〇(1/3)	〇(1/3)	2/27

「サイコロを3回振って、1または2の目が2回出る」場合は(a)、(b)、(c)の3通りあります。この3通りとも同じ確率2/27なので、この確率を3倍して、求める確率は2/27×3=2/9です。「3通り」である理由は、1または2の目が出る場合を3つの試行の中から2つ選ぶと考えればよいためです。3つの中から2つを選ぶ場合の数はいわゆる「組み合わせ」で、₃C₂=₃C₁=3です。上の表は、3つの中から2つ選ぶのも残りの1つを選ぶのも同じ通り数になる、ということのよい例になっています。

では最後に式の意味をもう一度考えることにします。試行n回中に事象Aがr回出る場合は、事象Aが何回目の試行で出るかの違いにより何通りかあるのですが、どの場合も同じ確率p^r×(1-p)^n-rになります。確率が同じなので、これに何通りあるかをかけることで、求める確率「試行n回中に事象Aがr回出る確率」がわかります。何通りあるかはn個の中からAがr個出る場所がある（組み合わせの考え方）と考えて、_nC_r通りです。したがって求める確率「試行n回中に事象Aがr回出る確率」は、_nC_rp^r(1-q)^n-rです。

<< 独立試行の確率　条件付き確率 >>

独立試行の確率

ある事象とある事象がお互いの確率に影響を与えないとき、これらの事象は「独立」だと言います。事象Aの確率をP(A)、事象Bの確率をP(B)とすると、事象Aと事象Bが独立のとき、事象Aと事象Bが共に起きる確率はP(A)・P(B)です。集合論の記号も使うとP(A∩B)=P(A)・P(B)と表現できます。確率論において試行は「起こりうる結果がいくつかあり、そのどれか一つが偶然で起こる流れ」のことで、試行の集まりが事象ですが、高校数学の確率を考える分にはそんなに気にしなくてもよい言葉だと思います。

独立とは別に「余事象」の言葉もあります。「確率」で対象にできるのは起こるか起こらないかはっきりする事象です。起こるか起こらないかのどちらかなので、起こる確率と起こらない確率を足すとすべての場合を網羅して確率は1です。起こる確率をpとすると、起こらない確率は全確率1からpを引いて1-pで表現できます。このpと1-pの組み合わせはよく使うので、この表現の仕方を覚えておくと割といろいろなところで役に立ってくれます。

ちょっとした具体例で上のことを確認しておきます。AとBのくじがあって、Aのくじで当たる可能性が1/4、Bのくじで当たる可能性が1/5だとします。下の三つの場合の確率を考えてみることにします。

1. Aで当たってBでもあたる場合。
2. Aで当たってBではずれる場合。
3. 少なくとも一方は当たる場合。

AのくじとBのくじは別々にあるので片方の結果がもう片方の結果に影響するなんてことはないでしょう。なので事象AとBは独立です。１では、「Aで当たる確率1/4」かける「Bで当たる確率1/5」=1/20の確率で、AとBのくじ両方に当たります。２ではAで当たる確率は1/4で、Bではずれる確率は1-1/5で4/5なので（余事象）、1/4×4/5で1/5です。３の「少なくとも」は確率の問題でよくみかける表現で、「少なくとも一方は当たる」の逆の現象にあたる余事象「両方ともはずれる」確率を1から引いてやるとでてきます。両方ともはずれる確率は

\begin{align} (1-\frac{1}{4})\cdot(1-\frac{1}{5})=\frac{3}{4}\cdot\frac{4}{5}\\ =\frac{3}{5}\\ \end{align}

なので、少なくとも一方は当たる確率は1-3/5=2/5です。３の事象は「AとBともにあたるまたはAであたってBではずれるまたはAではずれてBであたる」と言い換えることができるので、検算のためにこの確率を計算してみると

\begin{align} \frac{1}{4}\cdot\frac{1}{5}+\frac{1}{4}\cdot\frac{4}{5}+\frac{3}{4}\cdot\frac{1}{5}=\frac{1}{20}+\frac{1}{5}+\frac{3}{20}\\ =\frac{2}{5}\\ \end{align}

となり先に求めた値と一致しています。たいてい「少なくとも」の表現が入っている問題は「1-余事象の確率」で求めた方が楽ですので、その表現を見つけたらそちらのやり方でやってみてください。

<< 重複順列　反復試行の確率 >>

重複順列

後々の説明のために、確率の前に重複順列について説明しておきます。「n個の中から重複を許してr個順番に並べる並べ方」を重複順列と呼びます。この一文だとどういうことかわかりづらいので具体例で説明します。

A、B、C、D、Eの5個の中から3個選んで順番に並べる場合は順列です。一番目は5通りあって、二番目は一番目のものがなくなっているのでその各々に4通り、同じように三番目はさらに一つ減ってその各々に3通り、合計5×4×3=60通りあります。これに対して「重複を許して」というのは一度選んだものをまた選んでよいことを意味しています。ということで二番目以降も減らずに一番目と同じ5通り、三番目も5通りなので5×5×5=125通りです(図１）。以上より「n個の中から重複を許してr個順番に並べる」重複順列の並べ方はn×n×…×n（nをr個かける）=n^rです。

関連ページ：順列

数学の問題を解くうえではもうこれ以上話すことはありません。ただ、この後の事象が連続して起こる場合を考えるにあたって、順列の考え方を振り返っておくとよいことがある…かも。順列₅P₃は「5つの中から3つ選んで並べる」という一つの事象に思えます。しかし一番目を選んでその条件で二番目を選んでさらにその条件で三番目を選ぶので、「各番目を選ぶ」ということがすでに一つの事象で、これが連続して起こる複合的な事象にみえます。二番目を選ぶときは一番目をすでに選んだという条件のために一つ減るわけで、この後出てくる「条件付き確率」と同様の考え方に思えます。重複順列では一回目の結果が次以降の選び方に影響しないわけで、「独立試行」の場合に類似します。「場合の数」と「確率」の違いはありますが、高校数学の「確率」を一通りやり終わった後で振り返ってみると、何か発見があるかもしれません。

<< 組み合わせ　独立試行の確率 >>